Vorrei presentare un illuminante lezione del prof. Ruggero Bertelli sul tema degli indicatori statistici deterministici a confronto con i classici indicatori media e varianza.

VEDIAMOLA IN AZIONE
Se ipotizziamo un investimento che un anno guadagna il 10%, l’anno dopo perde il 10%, il terzo anno guadagna di nuovo il 10% e il quarto anno perde il 10%, a vostro avviso quale sarà il rendimento dell’investimento alla fine di quattro anni?
PENSATE ALLA RISPOSTA PRIMA DI CONTINUARE A LEGGERE…
Se avete risposto zero, forse non vi ricordate che i rendimenti non sono lineari, se perdo il 50% per tornare al valore iniziale devo fare il 100%, ovvero le perdite non sono uguali ai rendimenti necessari per recuperarle.
Se perdo il 10% per tornare alla pari devo fare quasi l’11%, come potete vedere dall’immagine qui sotto.
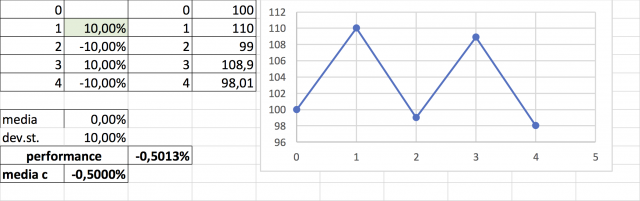
Dopo quattro anni mi trovo con circa 98 euro dai 100 iniziali, con un rendimento reale del -0,5% all’anno e con una volatilità del 10%-
Ma la cosa interessante è che la media dei rendimenti è uguale a zero, quindi se ho una serie storica che ha la media=0 è probabile che in realtà abbia perso dei soldi.
ADESSO FACCIAMO UN POCO PIU’ SUL SERIO
Facciamo un altro esempio, prendiamo una serie storica casuale dove al 50% può uscire un rendimento mensile +10% o -10% e lo interrompiamo dopo dieci anni misurando un rendimento complessivo positivo.
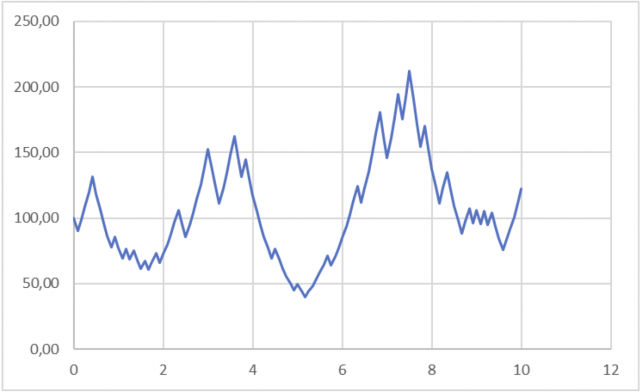
Se guardiamo i dati statistici ci accorgiamo che la media mensile è di 0,6% con una volatilità mensile del 10%, ovvero se annualizziamo i rendimenti abbiamo una media del 8% e una volatilità del 34%.
In realtà la serie storica ha avuto un rendimento medio annuo di poco superiore al 2%, non certo all’8% che in 10 anni avrebbe significato più del raddoppio del capitale.
Il problema, come si evince dalla tabella è che lo Sharpe Ratio (SH A nella tabella), sarebbe superiore al 0,2 mentre nella realtà sarebbe stato del 0,05, ovvero quasi nullo.
Viceversa il DIAMAN Ratio (DR nella tabella), spiegato in diversi post come Introduzione al DIAMAN Ratio, Fare Momentum con il DIAMAN Ratio e Strategia di TIMING con il DIAMAN Ratio essendo una serie storica molto variabile, è basso perché non c’è una chiara indicazione della tendenza futura.
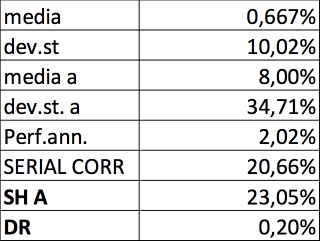
Ma se prendiamo una serie storica, sempre casuale e calcolata con il medesimo approccio casuale con rendimenti +10% e -10% che al termine dei 10 anni ha un rendimento negativo, i difetti degli indicatori media/varianza diventano palesi.
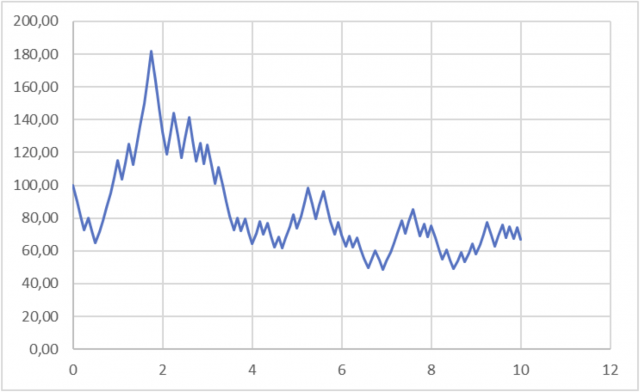
Mentre la volatilità rimane praticamente la stessa sia mensile che annuale rispetto all’esempio precedente (segno che il motore di simulazione Montecarlo ha fatto il suo dovere), la media mensile è positiva e di conseguenza quella annuale sembra anche decente (2% non si può definire buono come rendimento con una volatilità media annua del 34%).
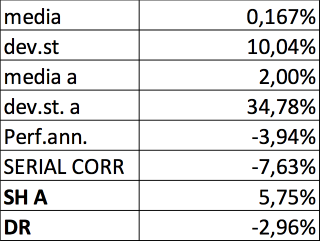
Nella realtà la performance media annua è negativa di quasi il -4% all’anno, quindi con una perdita finale molto elevata a discapito di indicazioni media/varianza positive, visto che lo Sharpe Ratio è seppur di poco positivo (0,05).
In questo caso il DIAMAN ratio è molto più aderente alla realtà, visto che il rendimento atteso che indica è di circa il -2,9% all’anno.
ADESSO FACCIAMO SUL SERIO
A questo punto con spirito indagatore il Prof. Bertelli ha realizzato due simulazioni Montecarlo generando 10.000 serie storiche dove la probabilità di avere un rendimento del +10% fosse del 50% e la probabilità di ottenere un -10% fosse anch’essa del 50%.
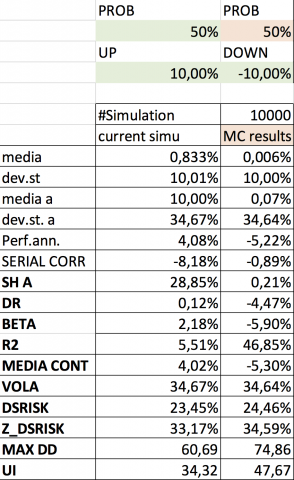
Da questa simulazione si evince che la media delle 10.000 simulazioni è zero, la volatilità mensile sempre del 10% e quindi annuale del 34%, mentre la performance media annua reale è di circa il -5% medio annuo.
Lo Sharpe Ratio è positivo, la Downside Volatility (DSRISK nella tabella) ovvero la parte negativa della volatilità è del 24%.
Il DIAMAN Ratio indica correttamente un -4,47%, quindi più aderente alla realtà, e l’Ulcer Index un valore di 47.
ULTIMA SIMULAZIONE
Adesso proviamo a guardare un’altra serie di 10.000 simulazioni Montecarlo dove non vi dico ex-ante quali sono i rendimenti positivi o negativi, lasciandovi indovinare a voi quale sia il rendimento configurato in caso positivo e in caso negativo (sempre al 50% di probabilità).
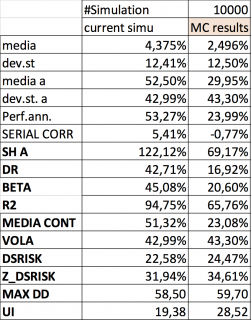
Se guardiamo e intendiamo la volatilità come indicatore di rischio invece che di incertezza, come da me spiegato nel POST…, queste 10.000 serie storiche, con una volatilità annualizzata del 43% sembrerebbe molto più rischiosa della precedente.
QUESITO
La media di rendimento è positiva, ma questa positività è dovuta all’aumento della volatilità oppure anche da una asimmetria dei rendimenti positivi e negativi?
Dagli indicatori media/varianza non è per nulla facile comprenderlo, mentre se guardiamo gli indicatori deterministici (ovvero il DIAMAN Ratio, lo Ulcer Index, la Down Side Volatility e il Drawdown possiamo carpire molte più informazioni utili.
Infatti la Downside Volatility è del 22%, leggermente inferiore della precedente nonostante l’incremento della volatilità denominando una chiara asimmetria.
INDICATORI DETERMINISTICI
Ma la superiorità degli indicatori deterministici si evince non tanto per il DIAMAN Ratio del 16% (che sconta ovviamente l’incertezza della serie storica evidenziata dal coefficiente di determinazione R2 che ha valore 67% di media), ma dall’Ulcer Index che è molto inferiore all’esempio precedente, evidenziando che questa seconda configurazione della simulazione montecarlo ha bisogno di molto meno tempo per recuperare il minimo precedente.
Provate a scrivere sui commenti quali sono i rendimenti positivi e negativi della simulazione e come ci siete arrivati.
Queste considerazioni, unite ai post Sharpe Ratio: i 4 difetti principali – parte 1 e Sharpe Ratio: i 4 difetti principali – parte 2 che ho scritto sui difetti dello Sharpe Ratio, evidenziano non tanto che l’indicatore inventato dal premio Nobel William Sharpe sia sbagliato, ma che sbagliato è il nostro modo di utilizzarlo, di fatti il suo utilizzo, come lo stesso Sharpe ha evidenziato in un paper del 1998, dal titolo “Morningstar’s Risk Adjusted Ratings” Il suo indicatore non è stato creato e non è utile per la selezione dei fondi comuni di investimento.
APPROFONDITE SEMPRE
Non ci credete? Beh prendetevi del tempo per leggere il suo paper e vi convincerete da soli senza dover credere a quello che vi dico io, come d’altronde bisognerebbe fare sempre quando si approcciano temi così delicati come la statistica finanziaria.
