Ricapitolando brevemente i primi due difetti dello Sharpe Ratio, elencati nel Blog della settimana precedente: Sharpe Ratio: i 4 difetti principali – parte 1 ricordo che l’utilizzo di tale indicatore per creare dei ranking di fondi è molto, direi troppo, sensibile alla definizione arbitraria del valore del Risk Free Rate, oltre anche alla sensibilità derivante dalla scelta, anch’essa arbitraria e non standardizzata, della frequenza di analisi dei dati, ovvero se si prendono dati giornalieri, settimanali o mensili per l’elaborazione.
Il terzo grosso difetto dell’indice di Sharpe, descritto anche in un suo paper, è che l’utilizzo di tale indicatore (che ricordo è stato creato per definire la Capital Asset Pricing Line) per definire l’efficienza di un fondo rispetto ad un altro, non funziona in caso di rendimenti negativi e vi spiego perchè:
Immaginate due fondi che hanno perso in un anno il 5% entrambi, solo che uno ha volatilità 5% e l’altro ha volatilità 25%, quali dei due sarà indicato come fondo più efficiente? se facciamo -5/5 = -1 e -5/25 = -0,20 l’indice di Sharpe è migliore per il secondo, ma non c’è logica in questo, poiché un fondo 5 volte più volatile non può essere considerato più efficiente dell’altro.
Inoltre si può arrivare ad un paradosso che avevo evidenziato ancora nel 2009, ovvero due fondi con perdite praticamente una doppia dell’altra, avevano il medesimo Sharpe Ratio poiché la volatilità del primo che aveva perso il doppio era praticamente doppia a quella del secondo; il grafico qui sotto evidenzia questa distorsione.
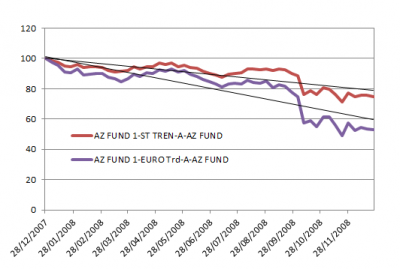
I due fondi, evidentemente gestiti con lo stesso identico approccio ma con leva diversa, hanno avuto nel 2008 uno Sharpe Ratio pari a -1,28 pur avendo perso il primo il 44% e il secondo il 22% circa.
Il quarto difetto, comune a tutti gli indicatori media/varianza che assumono che i mercati siano casuali (Quindi non deterministici) è che tale indicatore non cambia al variare della sequenza con cui si dispongono i rendimenti.
Per capirci se una serie storica ha un andamento del tipo -10% -10% -10% +10% +10% +10% avrà lo stesso Sharpe Ratio di una serie storica del tipo +10% – 10% +10% -10% +10% -10% +10% (e la stessa volatilità ovviamente), con l’unica leggera differenza che il Drawdown (perdita massima) della prima serie storica è stata superiore al 30%, la seconda di poco più del 10%, e questa differenza sostanziale un investitore la capisce molto bene.
Giusto per fare un’esempio del problema relativo agli indicatori non deterministici come lo Sharpe Ratio, se prendete una serie storica come quella del grafico di questo post che ripropongo per comodità
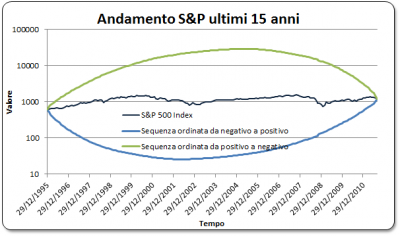
relativa allo S&P 500, se ordinate diversamente i rendimenti potrete ottenere quasi infinite serie storiche con una traiettoria diversa ma con media e varianza identica, quindi anche indice di Sharpe.
Nell’esempio sapere che analizzando un periodo di 190 rendimenti mensili possiamo avere 190! serie storiche con il medesimo Sharpe Ratio è un poco sconfortante.
Se non provate questa sensazione di sconforto è forse perché non sapete che numero sia il fattoriale di 190, ve lo riporto qui sotto giusto per rendervi l’dea
9680322675255249156123346514615331205418161260462873360750859919944104623425228207640470674933540169424682360525991982916161596983449594045525553704253602287443197783274656957056546338783001340434094795097553229620273057440272298773179365935914105128629426348958748638226084106818484328004851174161755668480000000000000000000000000000000000000000000000
Impressionante vero?
Se vi piace questo post, condividetelo con i vostri amici nei vari social…
a presto
DB

One comment
Comments are closed.