The concept of correlation and Daniele Bernardi’s vision.
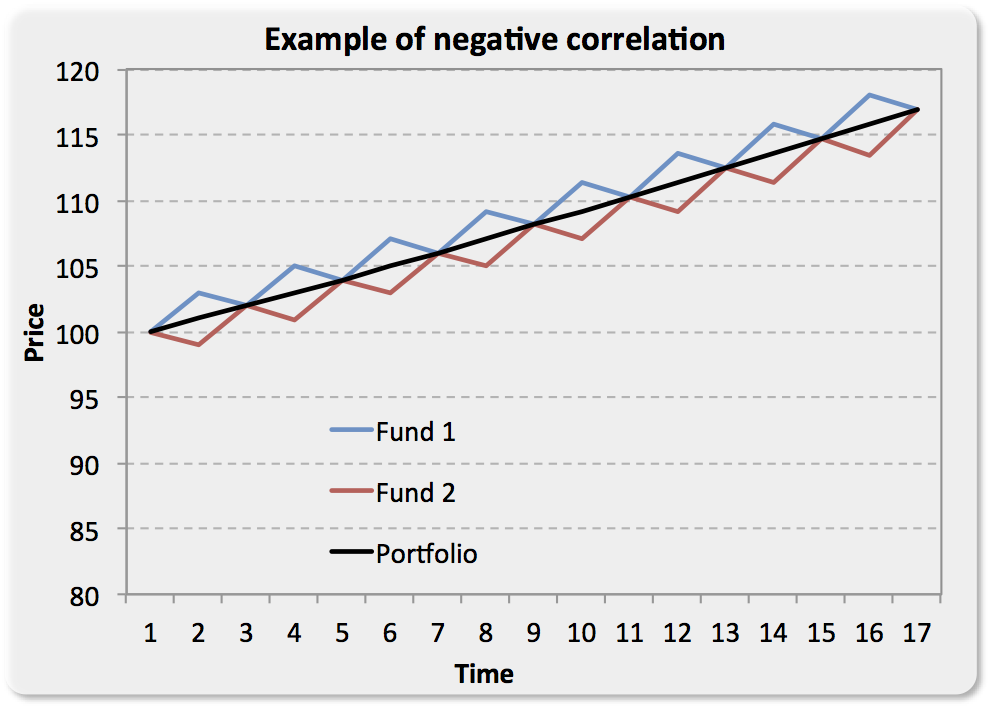
Everyone knows the concept of correlation, and everyone has surely seen a Cartesian plan where two funds are depicted growing over the long term, while in the short term are inversely related to each other as seen on the image above (on today’s post).
In 2009 I took part in a Risk Management course in London organized by Paul Wilmott (who also recently attended an annual conference of mine in Venice, www.quant.it) and Nicolas Taleb, author of best sellers Fooled by Randomness, and The Black Swan. Nicolas Taleb showed me (for the first time in my life) a graph like this:
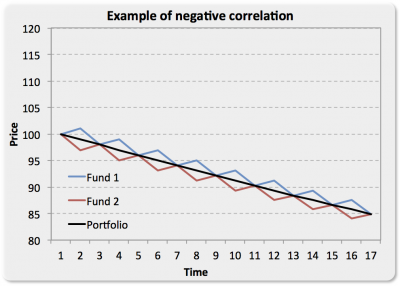
The correlation is negative in this case as well, but the funds are going down (following the same principle for which they should rise in the previous image).
This second image opened my eyes to how much we tend to overestimate negative correlation, because in fact it doesn’t necessarily generate a better performing portfolio, it may be more stable and less volatile, but not better performing than a positively correlated portfolio.
Allow me to explain. If I’ve invested in two funds with a correlation of 1, and the market is doing well and these are growing, will I get better or worse results than from a portfolio with two funds with a correlation of -1? The following is a graph that no one has shown me, therefore I’ve created:
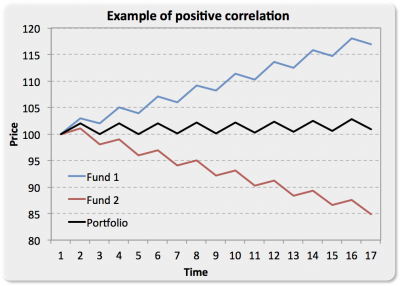
In this example the two funds are perfectly correlated amongst each other, but one goes up and the other goes down, impossible? Absolutely not, they are easily replicable on an excel sheet should you want to realize on your own how overestimated, often misused and misleading correlation can be – just like the matrices used to optimize portfolios with mean/variance models like Markowitz and others.
The reality is both asset managers and common investors, should aim to have instruments with correlation 1 when the markets go up and -1 when the markets go down. This is much easier said than done, but there is no other alternative if you really want to improve portfolio efficiency, any other use of a correlation, given that it itself changes in time, is useless.
I realize I am creating a sense of discomfort and discontentment in my readers who for years have studied and used correlations to create investment portfolios, but this is the hard truth.
I invite you to find those tools which allow for active correlation management, which is contingent upon an investment process that can either go Long or Short based on the market cycle, even if there are other great funds with which to compose more efficient portfolios.
Do so by looking at the strategy and the process, not the historical data.
